接地（アース）のことなら日本地工におまかせください。

6.接地抵抗測定

4）抵抗区域の例

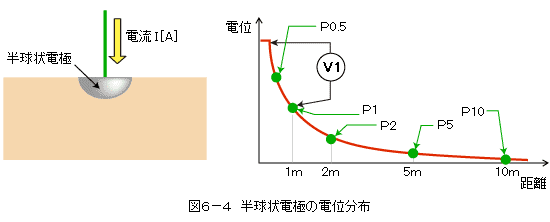
大地抵抗率100Ωｍの大地に半径0.1ｍの半球状電極が埋められていると仮定します。この時の半球状電極の接地抵抗は159.2Ω（以降、真値と呼びます）となります。この電極にＩ〔Ａ〕の電流を流した時、地表面に現れる電位分布を計算します。なお、電流補助極は無限遠点に配置するものとします。

表６−１　半球状電極の地表面電位分布

P点 ��	EからPまでの距離 〔m〕	電位差　E-P V1〔V〕	抵抗値 V1／Ｉ〔Ω〕	真値との誤差 〔％〕
P0.5	0.5ｍ	127.4V	127.4Ω	20.0％
P1	1ｍ	144.3V	144.3Ω	9.36％
P2	2ｍ	151.2V	151.2Ω	5.0％
P5	5ｍ	156.0V	156.0Ω	2.0％
P10	10ｍ	157.6V	157.6Ω	1.0％
P20	20ｍ	158.4V	158.4Ω	0.5％
P50	50ｍ	158.9V	158.9Ω	0.2％

接地抵抗値を測定する場合、表６−1のV1にあたる電位差（E極とP極の間の電位差）と電流から接地抵抗は算出されます。表からも分かるように、E極とP極の間隔を広く取るほど真値に近づくことがわかります。
例えば、表６−1における真値との誤差を見ると、5％以下とする場合のE極とP極の間隔は2ｍ以上となりますし、誤差を1％以下とする場合のE極とP極の間隔は10ｍ以上となります。このように、接地抵抗はその誤差範囲によりますが、接地極を中心とする有限の範囲（抵抗区域）内に収まっていると考えられます。
ただし、この抵抗区域及び電位分布曲線の形は、接地極の形状・大地抵抗率の大小・接地抵抗値等によって大きく変わります。